使用匈牙利算法求解任务分配问题
匈牙利算法(The Hungarian Algorithm)是一种在多项式时间内求解任务分配问题的组合优化算法。
关于任务分配问题,可以参考维基百科上的一个例子:
你有三个工人:吉姆,史提夫和艾伦。 你需要其中一个清洁浴室,另一个打扫地板,第三个洗窗,但他们每个人对各项任务要求不同数目数量的钱。 以最低成本的分配工作的方式是什么? 可以用工人做工的成本矩阵来表示该问题。例如:
| 清洁浴室 | 打扫地板 | 洗窗 | |
|---|---|---|---|
| 吉姆 | $2 | $3 | $3 |
| 史提夫 | $3 | $2 | $3 |
| 艾伦 | $3 | $3 | $2 |
在简单的数据和维度下,我们可以快速确认最优任务分配策略是:
- 吉姆清洁浴室
- 史提夫打扫地板
- 艾伦洗窗
一共花费 $6,这是我们最优的解决方案。
如果数据更加复杂,或者上升到更高的维度,该如何求解呢?使用匈牙利算法就可以快速求解出最优的任务分配方案。
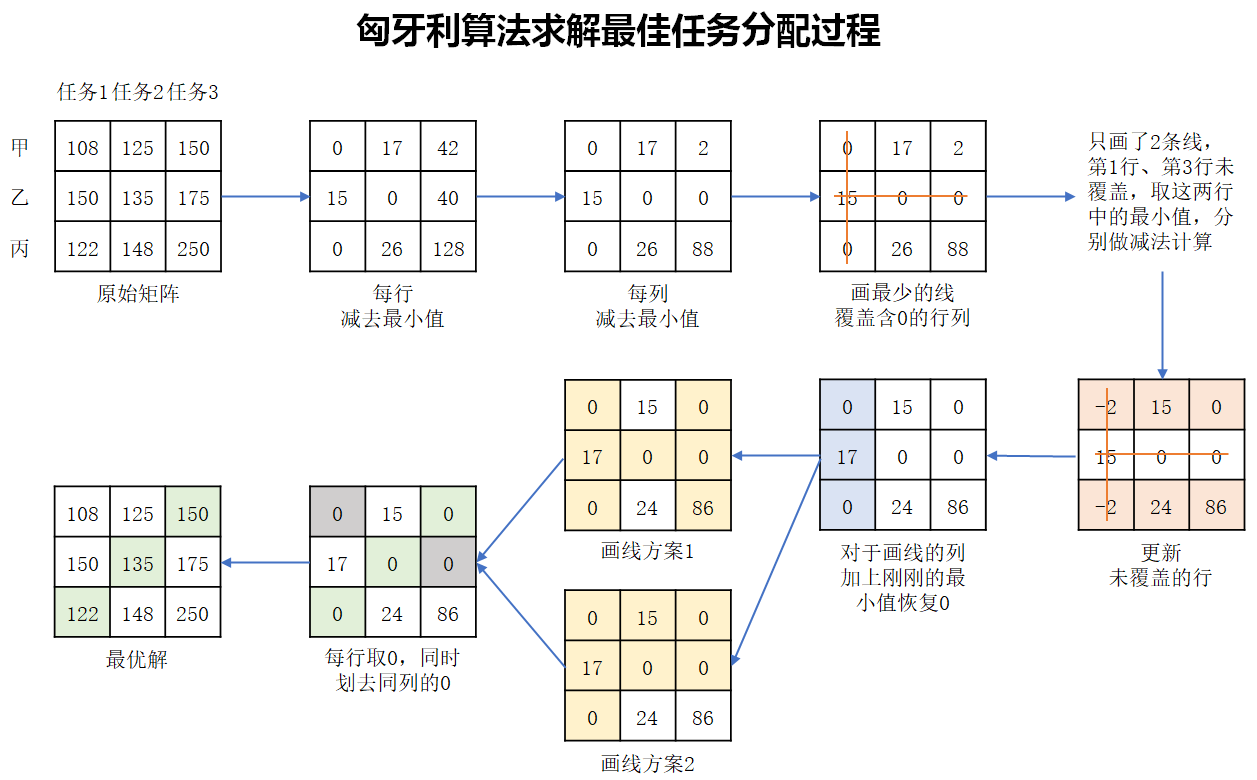
步骤和状态转换,在图中的例子写的非常清楚:
- 给出一个
n * n的矩阵,m[i][j]表示不同的人对不同的任务所要求的花费 - 针对每一行,选出最小值,并给该行的每个元素都减去这个最小值,可以得到一个新的矩阵
- 对于新的矩阵,针对每一列,同样选出最小值,并给该列的每个元素都减去这个最小值,可以得到一个新的矩阵
- 此时的矩阵中有些元素是
0,画最少的线来覆盖其中的0,如果线的条数就是矩阵的维度,此时就结束变换了(跳转到第 8 步),否则继续第 5 步 - 针对没有画线的行,挑出所有行中值最小的元素(不是每一行,是所有行),然后针对行元素做减法,得到新矩阵
- 针对画线的列,由于原来有
0,做减法后会出现负值,此时需要把刚刚减去的值给加回来,得到新矩阵 - 继续画线,直到线的条数与矩阵的维度一致(不一致,则跳转到第 5 步)
- 对于每一行,先找到只有一个
0的行,然后删除0元素对应的列上其他的0,重复,直到所有行都选出了0 - 对于筛选出来的
0元素,其对应的坐标映射到原始矩阵,就是我们的最优任务分配方案
References: